Question 1: Which number is larger: $n^{n+1}$ or $(n+1)^n$ for $n=2024$?
Question 2: Which number is larger: $e^{\pi}$ or ${\pi}^e$?
Answer 1: $n^{n+1} > (n+1)^n$ for $n=2024$.
Assume $n^{n+1} > (n+1)^n$ which is equivalent to $n$ > $\frac{(n+1)^n}{n^n} = (1+\frac{1}{n})^n$. The function $(1+\frac{1}{n})^n$ is a monotone increasing function, and it can be shown that $\lim_{n \to \infty}(1+\frac{1}{n})^n=e$, a well-known limit. Hence, it is clear that the statement holds for $n=2024$.
The proof of the limit follows from de l’Hospital: $\lim_{h \to 0}\frac{\ln(1+h)}{h}=1$. Replace $h$ with $1/n$ then this limit is equivalent to: $\lim_{n \to \infty}\frac{\ln(1+1/n)}{1/n}=1$. Let $x_n=n \cdot \ln(1+1/n)$ and we have $\lim_{n \to \infty}x_n=1$, and $\lim_{n \to \infty}e^{x_n}=e$ because $e^x$ is a continuous function. Therefore $\lim_{n \to \infty}(1+\frac{1}{n})^n=\lim_{n \to \infty}e^{x_n}=e$.
Source: Pythagoras Magazine
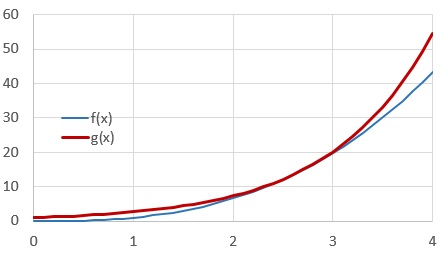
Answer 2: $\pi^e < e^{\pi}$, or $22.5 < 23.1$.
Let $f(x)=x^e$ and let $g(x)=e^x$.
We have $f’(x)=ex^{e-1}$ and $g’(x)=e^x$ , hence both functions are increasing for $x>0$.
We have $f’’(x)=e(e-1)x^{e-2}$ and $g’’(x)=e^x$ , hence the slope of both functions is increasing for $x>0$.
Both functions cross at $x=e$ and we have $f’(e)=g’(e)=e^e$. Also $f’’(e)=(e-1)e^{e-1} < g’’(e) = e^e$.
This means that the slope of $g$ is increasing faster than the slope of $f$ for $x=e$. It follows from proof by contradiction that $f(x) < g(x)$ for any $x>e$.